Sürekli değerlerle ölçümlenen nicel değişkenlerin yargılanmasında genellikle Parametrik yöntemler kullanılır. Bu yöntemlerde belli kuramsal dağılımlar çerçevesinde, verilerin gerçekten ölçümlenmiş düzeylerine dayanarak işlem yapılır.
Kitle – örneklem kıyaslaması, 2 örneklem kümesi arası kıyaslama, eşlendirilmiş konumlar kıyaslaması gibi yargılamalar için genellikle, normal dağılımı temel alan, Gosset’nin çeşitli “Student’s t” çözümleri uygun düşmektedir.
Aynı şekilde iki nicel değişken arasındaki bağıntının(ilişkinin) varlığı da genellikle Pearson-Bravais korelasyon katsayısı, “r” ile ortaya konmaktadır.
İkiden fazla kümenin kıyaslanmasında ise “Varyans çözümlemesi –ANOVA-” genellikle uygun olmaktadır.
Ancak söz konusu parametrik yöntemler, tüm durumlar için doğru seçenek değildirler ve uygun olmayan koşullarda kullanımları sonucunda “tipi hata” yani aslında geçerli bir savı ispatlayamama yönünde bir yanlışlıkla karşılaşılabilir.
Gerçekten de parametrik yöntemlerin kullanılabilmeleri için çeşitli koşullar gereklidir ve bunların yerine gelmediği durumlardaki uygulamaların sonuçları yanlış olabilir.
Araştırmacının, sürekli değişkenlerle gerçekleştirilmiş çalışmalardaki ilk sorgulaması, eldeki verilerin özelliklerine göre hangi tip yöntemin kullanılması gerektiği yönünde olmalıdır.
Daha güvenli olmaları nedeni ile parametrik yöntemler her zaman ana tercih olmasına karşın, koşullar uygun değilse kullanılmaları hata oluşturabileceğinden yerlerine uygun parametrik olmayan seçenek kullanılmalıdır.
Örneklem yetersizliği, değişkenin yapay nicelik (puan, skor, birim sayısı, vs) taşıması ve verilerin bazı bilinen dağılım tiplerine uyumsuz gözükmesi parametrik olmayan yöntemlerin seçilmesinde rol oynar.
Gerçekten de bu yöntemlerin bir diğer adı olan “Dağılımdan bağımsız yöntemler” terimi kuramsal dağılımların özelliklerine uyum zorunluğu taşımadıklarını gösterir.
Bir diğer adları olan “Sıra testleri” de verilerin gerçek oransal ölçüm düzeyleri ile değil, büyüklük sıralamaları ile ele alındıklarını belirtir.
Hemen hemen tüm parametrik olmayan yöntemlerde veriler küçükten büyüğe sıralanmakta ve bu sıralamada aldıkları sıra sayıları yöntemlerin uygulamasında kullanılmaktadır. Bu özellik ise uç değerlerin sonuçları aşırı etkilemesini engellemektedir.
Temel istatistik uygulamaları için parametrik yöntem kullanma koşullarına ve seçenek parametrik olmayan yöntemlere değineceğiz.
Kitle değeri ile örneklem kıyaslaması: Çeşitli çalışmalarda bir örneklemden elde edilmiş ortalamanın, kuramsal veya kritik değer kabul edilen veya belli şekilde elde edilmiş bir kitle ortalaması ile kıyaslanması amaçlanır.
Konu değişken sürekli özellikte ise, örneklem yeterli ise (n > 20) ve örneklemin değişim katsayısı (DK, CV) % 20’den küçük ise çözümleme uygun Student’s t (z) formülü ile yapılır.
Özellikle yapay nicel değişkenleri konu alan çalışmalarda, örneklem sayısı da kısıtlı ise bu tür kıyaslamalar için parametrik olmayan seçenek “İşaret testi” olacaktır. Bu test ile örneklemin bilinen veya kabul edilen bir kitle ortanca değerinden (Medyan) farklı olup olmadığı irdelenmektedir.
İki grup (örnek kümesinin) kıyaslanması: Sürekli değişkenleri konu alan çalışmalarda, örneklem sayıları yeterli (n > 30) kümelerin ortalamaları uygun Student’s t yöntemi ile kıyaslanır.
Daha düşük sayıda örneklem içeren 2 kümenin kıyaslanması süz konusu ise öncelikle küme varyanslarının eşitliği denetlenir (F yargılaması). Sonuçta varyanslar eşit bulunursa uygun Student’s yöntemi ile çözümleme yapılır.
Varyansların birbirlerinden farklı bulunduğu koşullarda veya değişkenlerin yapay nicellik taşıdığı çalışmalarda seçenek test, parametrik olmayan “Mann-Whitney U” yöntemidir. Yöntem, grupların ortalamalarını değil genel anlamdaki veri büyüklük düzenlerini(sıralarını) kıyaslar olarak düşünülmelidir.
İkiden fazla kümenin(grup) kıyaslanması (Tek yönlü varyans çözümlemesi): Tek yönlü varyans çözümlemesinin parametrik olmayan seçenek karşılığı “Kruskal Wallis H” testidir.
Grupların denek sayılarının yetersiz (n < 10) veya dağılımlarının aşırı saçkın veya değişkenin yapay nicellikte olduğu durumlarda kullanılmalıdır.
Tüm varyans çözümlemelerinde olduğu gibi, anlamlı sonuca erişilmesi durumunda, kümeler arası ikili kıyaslamaları yapmak için özel Post-Hoc yöntemler kullanılmalıdır. Benzer bir uygulama iki kümenin ortanca değerlerini kıyaslamak için de yapılabilir ve bu amaçla “Medyan” testi kullanılır.
Eşlendirilmiş (paired) diziler: Örneklem sayısının yetersiz olduğu (n < 20) ve farklar dizisi değişim katsayısının % 100’den büyük olduğu, sürekli değişkenleri konu alan eşlendirilmiş dizi çalışmalarında Student’s t uygulaması yanıltıcı sonuçlar verebilir.
Bu koşullarda -veya yapay nicellikteki değişkenlerde- eğer sadece 2 konum (eş) bulunuyorsa seçenek “Wilcoxon” testidir.
Mann-Whitney U testinin Wilcoxon testi olarak geçtiği kitaplarda, konumuz olan test ‘Wilcoxon İşaretli sıra testi’ olarak geçmektedir. Testin uygulanabilmesi için en az 6 örnek gerekmektedir.
Eşlendirilmiş konum(dizi/seri) sayısı 2’den fazla ise “Friedman” testi kullanılmaktadır. Bu testle genelde konumlar(diziler/seri) arasında bir farklılaşım olup olmadığı belirlenir. Eğer bir farklılık varsa hangi konumlar arasında bulunduğunu da saptamak için uygun çoklu kıyas yöntemleri kullanılır.
İlişki/Korelasyon: İki sürekli değişken arasındaki bağıntıyı belirlemek amacı ile kullanılan r katsayısı yargılaması, eğer değişkenler arasındaki fonksiyonel birliktelik doğrusallıktan uzaksa yanıltıcı sonuçlar verir.
Değişkenlerin dağılımlarının normallikten uzaklaşacak kadar saçkın olması (DK > %20) veya özelliklerinin yapay nicellikte olması da bağıntıyı r katsayısı ile yansıtmayı geçersiz duruma sokar.
Bu durumlarda seçenek, parametrik olmayan “Spearman r:rs” yöntemidir. Spearman r ile bağıntı soruşturulan araştırmalarda doğal olarak doğrusal regresyon soruşturmasına da girilmez.
Kısaca adlarına değindiğimiz parametrik olmayan bu yöntemler, araştırmalarda sık karşılaşılan, ikincil etkenlerin yok kabul edilebildiği istatistiksel uygulamalar (çift değişkenli-bivariate-çözümlemeler) için seçenek çözümleme yöntemleridir.
Aynı veri setleri için bir parametrik test ile parametrik olmayan karşılığının farklı anlamlılık durumları yansıtmasına rastlanabilir.
Araştırıcının kendi düşüncesi, beklentisi yünündeki testi seçmesi gibi bir durum bilimsel bir çalışmada akla bile getirilmemelidir.
Yukarıda değinilen koşullardan da anlaşılacağı üzere sürekli değişkenlere öncelikle parametrik yöntemler uygulayabilmek amacı ile yola çıkılır. Veri yetersizliği, saçkın veya belirsiz dağılımlar, değişken tipindeki özellikler, parametrik olmayan seçenek teste yönelmeyi getirir.
Sonuç olarak belli bir araştırma tasarımında, belli özellikteki veri setleri için ancak tek bir doğru çözüm seçeneği bulunmaktadır. Bunun parametrik veya non-parametrik seçenek olması ise açık ve nesnel koşullarla belirlenebilmektedir.
Çıkarsamalı istatistik, öncelikle bir veya daha çok kitle hakkında sonuç çıkarmak için iki yönüyle örneklem verisini kullanır. Çıkarsamalı istatistik de kullanılan iki yöntem vardır. Bunlar hipotez testi ve kitle parametrelerinin tahminidir.
Çıkarsamalı istatistik de, tek bir kitle veya iki ya da daha çok kitle arasındaki ilişkiler hakkında ön kestirimde(tahmin) bulunmak için hipotez tanımlanır. Hipotez testi örneklem verileriyle yapılan bir işlemdir ve yapılan hipotezi değerlendirmek için kullanılır. Genel olarak kullanılan hipotezler araştırma hipotezi ve istatistiksel hipotez olarak ikiye ayrılır.
Bir araştırma hipotezi, araştırmacının önceden söylediği genel bir durumu içerir.
Örnek-1, yeni doğan erkek çocukların ortalama kilosu üç kilodur, örnek-2, laboratuar ortamında beş ay boyunca belirli bir besin ile beslenen tavşanların doğal ortamda beş ay boyunca beslenen tavşanlardan daha kiloludur vs. gibidir. Buradaki birinci örnek tek bir kitleyi, ikinci örnek ise iki kitleyi temsil etmektedir.
Araştırma hipotezlerini değerlendirmek için iki istatistiksel hipotez kullanılır. Bunlar, H0ile gösterilen yokluk hipotezi ve H1 ile gösterilen alternatif hipotezdir. Yokluk hipotezi, etki yoktur veya fark yoktur ifadesidir. Araştırma hipotezinde genellikle çalışmaya göre etki vardır veya fark vardır beklentisi olduğu için araştırmacılar yokluk hipotezinin ret edilmesini beklemektedir.
Alternatif hipotez bir etki veya fark vardır durumunu göstermektedir. Bu nedenle araştırmacılar alternatif hipotezin desteklenmesini beklemektedirler. Örnek –1 için araştırma hipotezinde, erkek çocuklarının doğum ağırlıkları, N kitleden rasgele çekilmiş n tane erkek çocuğundan elde edildiği varsayılmıştır. Bu durumda, yokluk ve alternatif hipotezler:
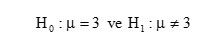
biçimine kurulur. Yokluk hipotezi, örneklemin temsil ettiği kitlenin ortalaması 3’e eşit olduğunu, alternatif hipotez ise 3’e eşit olmadığını gösterir.
Eğer etki yok ise örneklem ortalaması 3 eşit veya oldukça yakındır. Böyle bir sonuç elde edilirse araştırmacı, çekilen örneklemin ortalama değeri 3 olan bir kitleden geldiğine emin olacaktır.
Bir etki var ise, bu, örneklem ortalamasının 3’den oldukça aşağıda veya yukarıda olduğunu gösterecektir.
Böylece, örneklem ortalaması 3’den oldukça büyük veya küçük olduğundan araştırmacı, kitle ortalamasının 3’den farklı olduğu sonucuna ulaşır ve yokluk hipotezi ret edilir.
Buradaki alternatif hipotez iki yönlüdür. Yani, belirli bir yönde tahmin yapılmamış, 3’den küçük veya büyük olup olmadığı belli değildir.
Ancak belirli bir yönde tahmin yapılmak istenirse alternatif hipotez,
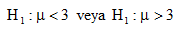
Biçiminde tek yönlü olarak kurulur.
Burada yokluk hipotezi ret edilir ise kitle ortalamasının 3’den küçük olduğuna, kabul edilir ise 3’den büyük olduğuna karar verilir.
Araştırmacı yukarıda verilen üç tane alternatif hipotezden sadece bir tanesini seçerek yokluk hipotezine karşı test etmek amacı ile kullanacaktır.
Araştırmacılar, iki yönlü veya tek yönlü alternatif hipotezi kullanacaklarına karar verirken, bazıları, bir denemenin sonuçları hakkında önsel beklentileri(bilgiler) dikkate almadan daima iki yönlü alternatif hipotezi tercih ederken, bazıları, önsel bilgi olmadığı zaman(bir etki veya farkın yönü ile ilgili beklenti yok ise) tek yönlü alternatif hipotezleri kullanmayı tercih etmektedirler.
Bazı araştırmacılar, bir farkın veya etkinin yönü hakkında belirli bir beklentiye sahip ise tek yönlü alternatif hipotez kullanmaktadır.
Tek yönlü alternatif hipotezi kullanmak yokluk hipotezini ret etmek için bir avantajdır.
Yukarıdaki açıklamalar ilk örnek, tek örneklem testleri için test edilmek istenen hipotezlerini içermektedir.
İkinci örnek ise iki örneklem testleri için oluşturulacak hipotezler aşağıda açıklanmıştır. Birinci grubu oluşturan tavşanlar laboratuvar koşullarında beslenenlerdir.
Bunlar birinci örneklemdir ve n1 tane tavşan vardır. İkinci grubu oluşturanlar doğal ortamda beslenenler, ikinci grubu oluşturur ve n2 tane tavşan vardır. Bu örnek için yokluk ve alternatif hipotez,
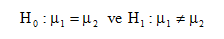
Biçiminde kurulur. Yokluk hipotezi, birinci örneklemin temsil ettiği kitlenin ortalaması ile ikinci örneklemin temsil ettiği kitlenin ortalaması eşittir demektir.
Daha açık ifade ile, laboratuvarda beslenen tavşanların ağırlıkları ile doğal ortamda yetişenlerin ağırlıkları arasında fark yoktur demektir.
İki yönlü kurulan alternatif hipotez, eşit olmadığını veya fark olduğunu göstermektedir. Bu durumda iki tavşan kitlesinden birincisi N1 tane, ikincisi N2 tane olmaktadır. Bir farkın veya etkinin bulunmaması, iki örneklem ortalamasının eşit veya birbirlerine yakın olduğunu gösterecektir.
Eğer böyle bir sonuç elde edilir ise örneklemler iki farklı kitleden elde edilmemiştir demektir. Bir etki bulunmuş ise, iki örneklem ortalaması arasında önemli bir fark gözlenmiştir demektir.
Böylece, yokluk hipotezini ret ederiz ve birinci örneklemin ortalaması ikinciden önemli derecede büyük veya küçük olduğunu söyleriz. Bu örnek için tek yanlı alternatif hipotezlerde kullanılabilir.
Hipotez testlerinde araştırmacılar için iki tür hata yapma olasılığı vardır. Bu hatalar I. tür hata ve II. tür hata olarak karşımıza çıkar.
I. Tür hata, yokluk hipotezi doğru iken test işlemi sonucunda ret edilerek alternatif hipotezin kabul edilmesi durumudur. I. Tür hata yapmanın olabilirliği bir deneyin değerlendirilmesinde araştırmacının kullandığı alfa düzeyi ile belirlenmiştir.
II. Tür hata, gerçekte alternatif hipotezin kabul edilmesi(doğru iken) gerekirken test işlemi sonucunda yokluk hipotezinin kabul edilmesi demektir. II tür hata yapmanın olabilirliği betaile gösterilir. Bununla ilgili özetleyici tablo aşağıdaki gibi verilir.
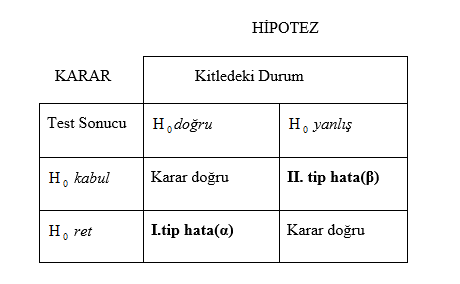
Bu iki tür hata arasında ters bir ilişki söz konusudur. Biri artarken diğeri azalır. Birinci tip hata testin anlamlılık(önemlilik) seviyesini ifade ederken, 1- istatistiksel testin gücünü ifade eder. Araştırmacılar genellikle a’yı 0.01 ve 0.05 anlamlılık düzeyini tercih ederler. Bu seviyeler, sırasıyla çok önemli, önemli anlamında kullanılır.
Bir hastanede doğan çocukların(oldukça çok-binlerce) %90’nın ağırlığı 2.6-3.8 kğ arasında olduğu bilinmektedir. Yeni doğan bir çocuğun ağırlığı 2.6’dan az ve 3.8 kğ’dan fazla olması olasılığı %10’dur.
Bu orana, a anlamlılık düzeyi olarak bilinir. %90 güven aralığını, %10 yanılma düzeyini gösterir. Bu hastanede doğduğu halde 4.5 kg ağırlığındaki bir çocuk hakkında ne diyebiliriz? Bu durumda nasıl bir sonuca ulaşırız?
Bu ortaya çıkan durum I. tip hata ve II. Tip hata ile ilgilidir. Bu hastanade doğan ve 4.5 kg gelen çocuk, %90 güven aralığı dışında yani %10’luk kesimde kaldığı için, bu hastanede doğmamıştır kanısına vardığımızda yaptığımız hataya I. Tip hata ortaya çıkmaktadır.
Bu çocuk bu hastanade doğmuştur ve diğerlerinden farksızdır biçiminde gerçek olan durumu reddetmek bilimsel olarak yanlış ve hatalıdır. Bu yanlış bir sonuçtur. Aslında doğru olan bir hipotezi reddetmek I. Tip hatayı meydana getirir.
Bu doğan çocuk ile daha önce doğan çocuklar(kitle) arasında fark yoktur Ho hipotezi red edilerek, gerçekte bir hata yapılmış ise, I. Tip hata yapılmış demektir. a=%10 alındığında, iki yönlü seçenek hipotez için alanın sağı ve solu %5’lik iki eşit parçadan oluşur.
Bebek bu hastanede doğmadığı ve ağırlık bakımından da bu kitleye ait olmadığı halde, bu çocuğu bu hastanede doğan çocuklar arasında kabul edersek bir hata yapmış oluruz ve bu hataya II.tip hata denir.
Bu hataya b tipi hata denir. Bu durumda çocuk bu hastanede doğmadığı halde, gerçeğe aykırı biçimde, bu çocuk ile hastanede doğan çocuklar arasında fark yoktur yargısına varıyoruz.
Analiz sonucu Gerçek durumun tam tersidir. Farklılık yoktur Ho hipotezini kabul ediyoruz. Ancak bu gerçekte doğru olan duruma ters bir durumdur. Ho hipotezinin kabul edilmesi gerçekte bir hata ise bu II. Tip hata demektir.
II. tip hata yapma olasılığı önceden düşünülmelidir. Bu olasılığı b adı verilir ve en yayğın olarak %10 veya %20 olarak kabul edilir. 1-b oranına da istatistiksel testin gücü denir.
Bu gücün %68’den büyük olmasına dikkat edilmelidir. Varılan yargıların bilimsel olup olmadığını belirleyen istatistiksel güçtür.
Güven aralığını veya 1-a düzeyini sabit tutarak örneklem sayısı artırılırsa testin gücü yükselir.
Kısaca Gerekli örneklem sayısı artırılırsa, Tip I ve Tip II hata azaltılmış demektir. I tip hatadan kaçınmak için a düzeyi %10 yerine %5 alınmalıdır. II. Tip hatadan kaçınmak için de b düzeyi düşürülmeli kısaca testin gücü artırılmalıdır.




