Bu yöntem 1932’de ABD-Chicago’da başlangıçta sermaye piyasalarıyla ilgili araştırmalar yapma amacıyla oluşturulan Cowles Komisyonu’nun çalışmalarına dayanır.(Charemza, 1997). Uzun yıllar boyunca ekonometrik araştırmalarda izlenen ve Gilbert (Gilbert, 1986 ) tarafından ‘ortalama iktisadi regresyon ‘ olarak da isimlendirilen bu yöntem şu şekilde işlemektedir.
Geleneksel ekonometrik yöntemde çıkış noktası olarak doğru olduğu önsel olarak kabul edilen, iktisat kuramından elde edilen bir matematiksel kalıp ele alınır ( Gilbert, 1986 ).
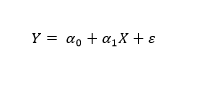
Burada amaç denklemde ‘in ve eğer kesişim katsayısı modele alındıysa ’ın tahmin değerlerini elde edilmektedir.
Ekonometrik modelin başarılı bir model olarak kabul edilmesi için hata terimi ile ilgili bazı varsayımların sağlanmış olması gerekir. Yani, hata terimiyle ilgili olarak, çoklu doğrusal bağlantı, değişen varyans, otokorelasyon gibi sorunların bulunmaması, ayrıca katsayıların istatistiksel açıdan anlamlı olması , modelin iktisadi beklentilere uygun olması gerekir.
Ancak başarılı bir tahmin modeli elde edilse dahi geleneksel yöntemle ilgili kuramsal bir sorun her zaman vardır.
Şöyle ki; aynı veya birbirine yakın iki veri seti kullanılarak , aynı konuyu açıklama amacı güden ancak temelinde farklı bir iktisadi düşünceyi hareket noktası olarak alan bir başka model ( ya da modeller ) olabilir.
Bu durumda aynı iktisadi kavramı ( değişkeni) başarılı bir şekilde açıklayan fakat temel aldığı iktisadi kuramlarda farklılaşan birden çok model ortaya çıkacaktır.
Birbirine zıt düşünceleri aynı veya benzer veri setiyle doğrulayan modellerin literatürde yer alması, bu çalışmaların bilimselliğiyle ilgili şüpheler doğmasına neden olabilir.
Bu sebeple; geleneksel ekonometri yöntemleriyle ilgili temel sorun ekonometriye, doğruluğuna inanılan bir iktisadi kuramın, veriler yardımıyla kanıtlanması amacına yönelik olarak başvurulan bir disiplin olarak yaklaşılmasıdır. ( Gilbert, 1986).
Dolayısıyla farklı araştırmacılar tarafından belirli görüşleri desteklemek amacıyla hazırlanan modeller ekonominin gerçek durumu ve ekonomik değişkenlerin aralarındaki etkileşimleri hakkında sağlıklı bilgi vermeyebilir. Geleneksel ekonometri yöntemlerinin bu eksik tarafını gidermek amacıyla önerilen alternatif yöntemlerinin en önemlilerinden biri genelden özele modelleme yöntemidir ( Darnell , Evans , 1990).
Genelden özele modelleme yöntemi, ya da diğer adıyla Hendry yönteminde amaç iktisadi kuramın öngördüğü tüm değişkenleri gecikmeli değerleriyle birlikte içeren geniş kapsamlı bir genel modelden, veri setiyle tutarlı, belirli kriterleri sağlayan mümkün olan en dar modele ulaşılmaktadır.
Modelleme süreci dört aşamadan oluşur. İlk olarak içerdiği değişkenler iktisat kuramının önerdiği denge ilişkileri ile örtüşen, sürecin dinamiği mümkün olduğunca düşük sınırlayan genel model formüle edilir.
Model, birbirine mümkün olduğunca dik, açıklama gücüne sahip ve iktisadi açıdan yorumlanabilecek niteliklere sahip değişkenler kullanarak yeniden parametrelendirilir. Model basitleştirilerek veri setiyle uyumlu en küçük versiyonu bulunur. Sonuçta ulaşılan modelin tahmin gücü üzerinde analizler yapılır ( Pagan,1987:4).
İlk aşamada kurulacak olan genel model konusunda dikkatli olmak gerekir. Çünkü bu model, çalışmanın ilerdeki aşamalarında kullanılacak olan tüm basitleştirilmiş modellerin yuvalandığı ve bu modellerin karşılaştırılacağı anahtar model görevi görmektedir ( Pagan, 1987) . Bu modelin oluşturulmasında kullanılacak rehber, ekonomi kuramı olacaktır.
Ekonomi kuramında, incelenen bağımlı değişkenin üzerine ortaya atılan görüşler doğrultusunda tüm olası açıklayıcı değişkenler tespit edilir. Bu değişkenlerin ve bağımlı değişkenin, gecikmeli değerleri açıklayıcı değişken olarak modele alınır. Genel modelin formu şu şekilde olmalıdır.
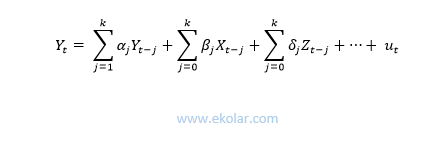
Burada k’nın yani gecikme sayısının belirlenmesi aşamasında serbestlik derecesinin fazla azalmamasına dikkat edilmelidir. Diğer yandan dinamik iktisadi süreci açıklayacak kadar da geriye gitmek gerekir.
Genel modeli kurarken önemli olan işte bu dengeyi kurmaktır. En uygun gecikme sayısının belirlenmesi için tahmin edilen modellere ait Akaike bilgi kriterleri v.b. kullanılarak gecikme sayıları belirlenir.
Hendry yöntemi’nin diğer bir aşamalarında genel modelde yeniden parametrelendirme ve basitleştirme işlemleri yapılarak en basit , en uygun modele ulaşılacaktır. Ancak elde edilen basit modelin uygun olup olmadığına nasıl karar verilecektir?
Diğer bir deyişle daha iyi bir modelin olup olmadığı kuşkusunu taşımadan en uygun modele ulaşıldığına nasıl karar verilecektir? Bu sorulara yanıt verebilmek için Hendry ve Richard ‘ ın önerdiği kriterlerin sağlanıp sağlanmadığına bakmak gerekir. ( Hendry ve Richard, 1982; Darnell ve Evans, 1990 ).
Model veri kabullü olmalıdır. Tahmin denkleminden elde edilen tahmin değerleri mantığa uygun olmalıdır. İktisadi olaylar hakkında birçok farklı yorum yapılmış, farklı kuramlar geliştirilmiştir.
Ancak elde edilen model, en azından bir kuram ile uyumlu olmalıdır. Modelde kullanılan açıklayıcı değişkenler en azından zayıf dışsal olmalıdır. Zayıf dışsal terimi açıklayıcı değişkenlerin hata teriminden bağımsız olması durumunu ifade eder.
Zayıf dışsal olmayan açıklayıcı değişkenler, normal olarak içseldir ve bu değişkenlerin kullanılması durumunda bir eşanlı denklem sistemi kurmak gerekebilir ( Gilbert, 1986 ).
Uygun model parametre değişmezliği sergilemelidir. Yani modelin farklı dönemler için tahmin edilmesi durumunda tahmin edilen parametreler, her dönem için aynı olmalıdır. Bu nokta özelikle öngörü ve politika belirleme amacı taşıyan modellerde çok önemlidir.
Çünkü bu iki ekonometrik amaç, belli bir dönem için tahmin edilen parametrelerin tahmin dönemi sonrası içinde geçerli olmasını gerektirmektedir. Model veri uyumluluğu sergilemelidir.
Modelden tahmin edilen değerler ile gözlenen değerler arasındaki farkların oluşturduğu seri temiz dizi sürecine sahip olmalı yani hata terimi rassal olmalıdır.
Uygun model diğer rakip modelleri içeriyor olmalıdır. Bu durumda model rakip modellerin sonuçlarını ve eksikliklerini içeriyor demektir.
Yukarıdaki kriterler elde edilecek olan nihai modelin sağlanması gereken kriterlerdir.
Ancak burada genelden özele basitleştirme sürecinde nelere dikkat edileceği sorusu ortaya çıkar. 9.7.2. model formunda, 6 açıklayıcı değişkenin 5 dönem gecikmeli değerlerini modele katan bir genel model ele alalım.
Böyle bir modelde 30 (=6×5) tane açıklayıcı değişken olacaktır. Bağımlı değişkenin gecikmeli değerlerinin veya kukla değişkenlerin kullanılması durumunda bu sayı artabilmektedir.
Bu modeli basitleştirme işlemi sırasında araştırmacının dayanağı ne olmalıdır ? Bu sorunun yanıtı modelin amacıyla yakından ilgilidir.
Örneğin basitleştirilecek olan modeldeki dışsallık durumları modelin amacına bağlı olarak önem kazanmaktadır.
Genelde yapısal analiz amaçlı hipotez testleri için zayıf dışsallık yeterli olurken öngörü amaçlı çalışmalarda güçlü dışsallık, politika belirleme amacı taşıyan modellerde ise süper dışsallık gerekmektedir.
Bu nedenle hata terimi ve açıklayıcı değişkenler arasındaki bağlantıların dereceleri dışlanacak veri seçiminde belirleyici olabilir. ( Gilbert, 1986).
Dikkat edilmesi gereken diğer bir nokta kurulan modelin sadece gözlenen dönemde değil, gözlem aralığı sonrasında da geçerli olmasını sağlanmasıdır.
Model kullanılarak yapılan öngörüler veya politika analizleri kullanılan değişkenlerin gelecekteki değişimlerinden olumsuz etkilenmemelidir.
Basitleştirme sürecinde göz önünde bulundurulması gereken bir başka konu elde edilen parametrelerin yorumlanabilirliği konusudur.
Tahmin edilen parametrelerin uzun dönem ekonomik ilişkiler açısından anlamlı kullanılabilir nitelikte olabilmelidir. Herhangi bir olguyu açıklamak üzere kurulan modellerden birkaçı birbirine yakın açıklama gücüne ve yeterliliğe sahip olabilir.
Böyle bir durumda yapılması gereken en basit olan model tercih edilmelidir. Bu sayede serbestlik derecesi daha yüksek olan model kullanılmış olur.
Mümkün olduğunca az sayıda açıklayıcı değişkenin kullanılması bu değişkenlerin birbirine dik olması olasılığını güçlendirecektir. Ayrıca daha basit model, modeli kullanılanlar için de daha anlaşılır olacaktır.
Yukarıdaki kriterlere göre yapılacak basitleştirme işlemi sırasında önerilen her yeni modelde yapılan kısıtlamanın geçerliliği F testi kullanılarak sınanmakta, yapılan basitleştirmenin istatistiksel açıdan uygun olup olmadığı modelin açıklama gücünü azaltıp azalmadığı test edilir.
Burada amaç, modelin sahip olduğu açıklama gücünü mümkün olduğunca korumaktır. Basitleştirme süreci sonunda ulaşılan özel modelin kabulü için bazı testler yapılmaktadır.
Özel modelde yer alan açıklayıcı değişkenlere ait katsayıların istatistiksel olarak anlamlı katsayılar olması gerekmektedir. Bunun test edilmesi için bu katsayılara Student- t testi uygulanır.
Değişen varyans sorununun incelenmesi için White ve Arch testi, spesifikasyon hatalarının tespiti için Reset testi, modelde otokorelasyon olup olmadığının tespit edilmesi için LM testi özel modelin uygunluğunun araştırılması için başvurulan diğer testlerdir.
Ayrıca tahmin edilen özel modelin daha önce yapılan rakip modellerin sonuçlarını da içeriyor olması beklenir. Bunun tespiti için yuvalanmış ya da yuvalanmamış testlere başvurulur.
Tüm bu testler sonucu iktisadi, istatistiksel ve ekonometrik yönden uygun olduğuna karar verilen özel modelin katsayıları iktisadi bilgileri verecek güce sahiptir. ( Çelem, 2003).




