Aynı koşullar altında tekrarlanan bir rassal deney veya gözlem sonuçları olumlu-olumsuz, başarılı-başarısız, geçerli-geçersiz gibi yalnız iki şekilde ele alınsın. Bu tür deneylere Bernoulli deneyi denir. Bu isim (1654-1705) Bernoulli’den sonra verilmiştir.
Bernoulli Dağılımının Tanımı: x rasgele değişkeni için iki olanak varsa (olumlu-olumsuz, başarılı-başarısız, … vb.) x’e Bernoulli değişkeni denir.
x rassal değişkeni, bir deneyin sonucu olumlu ise “1” değil ise “0” şeklinde tanımlandığında, bir deneyin başarılı sonuçlanma olasılığı p iken, x’in olasılık fonksiyonu;
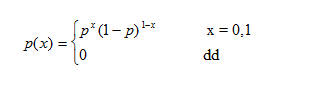
Bu fonksiyona “Bernoulli dağılımı” ve x’e Bernoulli dağılmış bir rassal değişken denir. Dağılımın “p” ile gösterilen tek parametresi vardır.
Aşağıdaki deneyler Bernoulli rassal değişkenleri ile ilgilidir.
- Paranın atılması.
- İçinde M siyah, N beyaz top bulunan bir kavanozdan top çekilmesi.
- Kusurlu ve kusursuz parçaların bulunduğu bir kutudan bir parçanın çekilmesi.
BERNOULLI DAĞILIMININ OLASILIK FONKSİYONU
P(x=1)=p
P(x=0)=1-p=q veya f(x)=P(X=x)=px.(1-p)1-x, x=0,1
BERNOULLI DAĞILIMININ OLASILIK YOĞUNLUK FONKSİYONU OLDUĞUNUN İSPATI
Bernoulli dağılımı kesikli bir dağılımdır. Olasılık yoğunluk fonksiyonu olması için;

BERNOULLI DAĞILIMININ MOMENT ÇIKARTAN FONKSİYONU
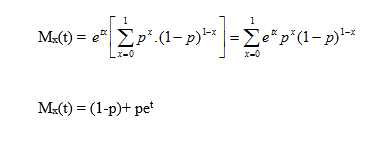
BERNOULLI DAĞILIMININ SIFIR ETRAFINDAKİ MOMENTLERİ

BERNOULLI DAĞILIMININ ARİTMETİK ORTALAMA ETRAFINDAKİ MOMENTLERİ

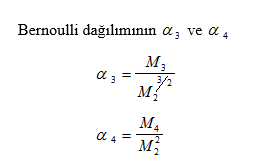
BERNOULLİ DAĞILIMININ BEKLENEN DEĞERİ VE VARYANSI





