Bugün elde edilen para, gelecekte elde edilecek aynı tutardaki paradan her zaman için daha değerlidir. Bunun nedeni, paranın bir zaman değeri olmasıdır.
- Birinci faktör, gelecekte elde edilmesi umulan para gerçekte elde edilmeyebilir (risk unsuru)
- İkinci faktör, bugün elde edilen para tüketim için harcanıp onun faydasından yararlanılabilir, ya da bugün elde edilen para ile yatırım yapılıp toplam servetin artırılması sağlanabilir.
PARANIN GELECEKTEKİ DEĞERİ VE BİLEŞİK FAİZ
Bileşik faiz (compound interest) en basit tanımıyla faizin de faizinin hesaplanması demektir. Basit faizde ise, faiz her dönem için ana para üzerinden hesaplanır.
Örneğin, 1.000 TL için yıllık %30 faiz oranı üzerinden iki yıllık bir dönem için basit faiz hesaplanırsa,
birinci yıl için 1.000 x %30= 300 TL faiz,
ikinci yıl için yine 1.000 x %30= 300 TL faiz hesaplanır.
Bileşik faizde ise, yani faizin de faizinin hesaplandığı sistemde
birinci yıl için faiz 1.000 x %30 = 300 TL,
ikinci yıl için 1.300 x %30 = 390 TL.
İki yıl için yatırılan 1.000 TL, %30 yıllık faiz oranından
Basit faiz hesabına göre dönem sonunda toplam
(1.000+300+300) 1.600
Bileşik faiz hesabına göre toplam (1.000+300+390) 1.690 TL’ye baliğ olmaktadır.
Burada 1.690 TL
- 1000 TL’lik ilk yatırım tutarı,
- 300 TL’lik ilk yılın faizi,
- 300 TL’lik ikinci yılın faizi,
- 90 TL birinci yılın faizi 200 TL üzerinden hesaplanan faiz.
1.690 TL.
Söz konusu 1.000 TL bileşik faiz hesabına göre 3 yıl için yatırılmış olsaydı;
2.197 = 1.690 (1+ %30)
= 1.300 (1+%30)(1+%30)
= 1.000 (1+%30)(1+%30)(1+%30)
= 1.000 (1+%30)3
= 1.000 x 1.303
= 1.000 x 2,197
Paranın gelecekteki değeri = An = A0 (1 + i)n
(A0)tutarındaki bir paranın (i) faiz oranı üzerinden (n) yıl için
Bir yıldan kısa süreler için bileşik faiz hesaplamak için faiz oranının ve dönemin faizin bir yılda kaç kez hesaplandığı sayısına göre düzeltilmesi gerekir.
Faizin bir yılda kaç kez hesaplandığı sayısını (m) ile gösterirsek bir yıldan kısa vadeler için bileşik faiz formülü aşağıdaki şekilde yazılır.
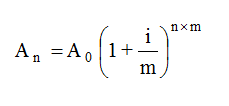
Örneğin, 1.000 TL’yi aylık %2,5 (yıllık %30) faiz oranından 1 yıl için yatırılmış olsun. Bir yıldan kısa süreler için bileşik faiz hesapları faizin yıl içinde kaç kere hesaplandığı sayısı dikkate alınarak aynı yukarıda yapıldığı gibi uygulanır ve 1.000 TL’sının aylık %2,5’den 1.yılın sonunda ulaşacağı tutar yaklaşık 1.3448 TL olarak bulunur.
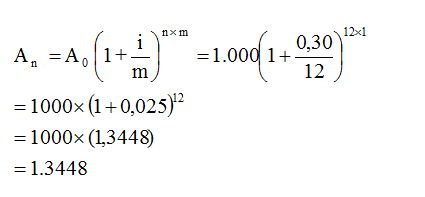
Ancak, unutulmaması gerekir ki, aylık %2,5 faiz oranının bileşik olarak yıllığı
12 x %2,5 = %30 değildir
(Eğer öyle olsaydı An 1.3448 TL yerine 1.000 x 0,30 =1.300 TL olarak bulunacaktı).
Bu durumda efektif faiz oranının hesaplanması gerekir. Birinci aşamada yıllık faiz oranı, faizin kaç kez bileşik hesaplandığı sayıya bölünür. İkinci aşamada, sonuca 1 ilave edilip bunun faizin kaç kez bileşik hesaplandığı sayısı kadar üssü alınır. Üçüncü aşamada, ikinci aşamada ilave edilen 1 düşülür.

Burada, (m) yine faizin kaç kez bileşik hesaplandığı sayısını belirlemektedir.
Yukarıdaki örnekte yıllık %30 olarak (aylık %2,5) kota edilen faiz oranının yıllık efektif oranı:

Örneğin, 6 ay vadeli mevduata yıllık bazda %20 faiz uyguladığını söyleyen bir banka, aslında 6 ay için uyguladığı faizin %10 olduğunu söylüyordur. Ancak bu 6 aylık %10 efektif olarak yıllık %20 oranına denk gelmez. Bu durumda efektif faiz:
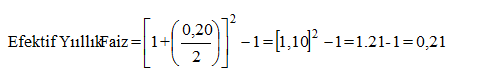
olarak hesaplanır.
Örneğin,
(A) bankası yıllık mevduata %19 faiz,
(B) bankası aylık mevduata yıllık %18 faiz ve
(C) bankası üç aylık mevduata yıllık %17 faiz uyguluyor ise, bileşik efektif olarak en cazip oran hangisidir?
(A) bankası için:
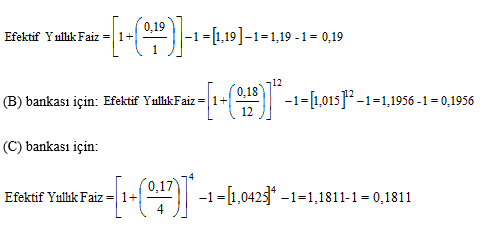
PARANIN BUGÜNKÜ DEĞERİ VE ISKONTOLAMA
Paranın gelecekteki değeri, bugün belli bir faiz oranından n dönem için yatırılan paranın dönem sonunda ulaşacağı tutarı ifade etmektedir.
Paranın bugünkü değeri ise, gelecekte elde edilecek paraların belli bir indirgeme oranı üzerinden bugün için tutarının ne olduğunu ifade eder.
Örneğin, 1.000 TL sının %30 faiz oranı üzerinden birinci yılın sonunda ulaşacağı tutarın 1.300 TL olduğunu biliyoruz.
An = A0 ( 1+ i )n = 1.000 (1+0,30)= 1.300 TL.
An = A0 ( 1+ i )n
1.200 = A0 (1.20)1
A0 = 1.200 / (1.20) = 1.000 TL
Dolayısıyla, genel olarak paranın bugünkü değerini veren formül:

ÇOKLU NAKİT AKIMLARINDA PARANIN GELECEKTEKİ VE BUGÜNKÜ DEĞERİ
Örneğin, bugün için bir yıllık %30 faiz ödeyen bir vadeli hesaba 1.000 TL yatırdığınızı ve bir yıl sonra aynı hesaba 3.000 TL daha yatıracağınızı varsayalım. Faiz oranlarının değişmediği varsayılırsa ikinci yılın sonunda elinize geçecek toplam tutar 3.840 TL olacaktır.


Çoklu nakit akımlarının bir yılı aşmayan vadelerde
Örneğin, aylık %1,66 (yıllık %20) faiz ödeyen vadeli bir hesaba birinci ay 300 TL, ikinci ay 400 TL ve üçüncü ay 500 TL yatırıldığını varsayarsak, üçüncü ayın sonunda ulaşılacak tutar:
300 x (1.0166)3 = 300 x 1,05063 = 315,18
400 x (1.0166)2 = 400 x 1,03347 = 413,39
500 x (1.0166)1 = 500 x 1,01666 = 508,30
Toplam gelecek değer = 1236,87 olur.
ANNÜİTELERİN GELECEK VE BUGÜNKÜ DEĞERİ
Finansal çalışmalarda dönemler itibariyle eşit tutarlardaki nakit akımları annüite olarak adlandırılır ve bu şeklindeki nakit akımları için bileşik faiz ve bugünkü değer faktörleri her 1 TL için çeşitli faiz ya da indirgeme oranlarından hesaplanıp tablo haline getirilmiştir.
Annüitelerin Gelecek Değerinin Hesaplanması:
Örneğin, 4.yılın sonunda 10.000 $’lık bir nakit paraya ihtiyacınız olacağını düşünelim. Yıllık dolar hesabınıza %3 faiz kazanacağınızı biliyorsanız, her yılın sonunda yatıracağınız 2.391 dolarla bu tutara ulaşmanız mümkün mü?
Annüite şeklindeki nakit akımları için gelecek değer faktörü aşağıdaki formül yardımıyla hesaplanır.

Annüiteler şeklinde her yıl sonu itibariyle dört kez yatırılan 2.391 dolarlık nakitlerin gelecekteki değeri, bu tutarın annüitelerin gelecek değer faktörü ile çarpılmasıyla elde edilir.
Annüitelerin gelecek değeri= 2.391 x 4,1836= 10.002,98 Annüitelerin Bugünkü Değerinin Hesaplanması:

Aynı sonuca 3.000 TL’lık nakit akımlarının her yıl için ayrı ayrı bugüne getirilmesi şeklinde de ulaşmak mümkündür. Bu durum için hesaplamalar aşağıdaki şekilde yapılır:
3.000 x 1/ 1,23 = 3.000 x 0,5787 = 1.736,1
3.000 x 1/ 1,22 = 3.000 x 0,6944 = 2.083,2
3.000 x 1/ 1,21 = 3.000 x 0,8333 = 2.499,9
Bugünkü değer toplamı = 6.319,2
Örneğin, kullandığınız bir tüketici kredisi için bir yıl buyunca her ay bankaya 500 TL yatırıyorsanız ve bankanın tüketici kredileri için uyguladığı faiz aylık %2,3 ise ödenen tutarların bugünkü değeri aşağıdaki şekilde hesaplanır.
Annüitelerin bugünkü değeri = annüite tutarı x annüite B.D. faktörü
= 100 x [ 1- (1/1.023)12]/0,023
= 100 x (1-0,7612)/0,023
= 100 x 10.383
= 5.191,50
Örneğin, bankadan aylık %1,8 faiz oranından, 48 ayda geri ödemeli 100.000 TL tutarında bir konut kredisi alındığını varsayalım.
Söz konusu krediler için annüiteler şeklinde her ay geri ödenecek tutarın ne olduğunu bulmaya çalışalım. Bu takdirde yukarıdaki formülde annüitelerin bugünkü değeri bilinmekte ancak annüite tutarları aranmaktadır.
Annüitelerin bugünkü değeri = annüite tutarı x annüite B.D. faktörü
100.000 = annüite tutarı x [ 1- (1/1.018)48]/0,018
100.000 = annüite tutarı x (1-0,4247)/0,018
100.000 = annüite tutarı x 31.9597
annüite tutarı = 100.000 / 31.9597
annüite tutarı = 3.128 TL
Dolayısıyla, söz konusu konut kredisi için 48 ay boyunca her ay 3.128 TL ödenecektir.




